一致性Hash常用于分布式缓存系统或负载均衡，将Key值/请求映射到具体机器IP上，并且增加和删除1台机器的数据移动量较小(不是没有）。

以分布式缓存系统为例，比如你有 N 个Redis 服务器，那么如何将一个对象Key映射到 N 个Redis上呢，你很可能会采用类似下面的通用方法计算Key 的hash值，然后均匀的映射到到N个cache。

求余算法: hash(Key)%N

那这种计算方法有什么问题呢？

1. 一个 Redis 服务器挂掉了，这样所有映射到这台redis服务器的对象都会失效。如果需要把这台Redis服务器 从Redis集群中移除，这时候Redis服务器是 N-1 台，那么对应映射公式变成了 hash(Key)%(N-1) ；
2. 还有一种情况是由于访问量增多，需要添加Redis服务器，这时候Redis是N+1台，映射公式变成了 hash(Key)%(N+1) ；

这意味着突然之间几乎所有的Redis缓存都失效了，所有的访问都会直接冲向数据服务器(引发缓存击穿），对数据服务器造成压力，甚至是数据服务器瘫痪。

如何解决上面的问题呢？一致性Hash算法就派上用场了。

Hash环

一致性Hash算法也是使用取模的方法，只是，刚才描述的取模法是对服务器的数量进行取模，而一致性Hash算法是对2^32取模，什么意思呢？简单来说，一致性Hash算法将整个哈希值空间组织成一个虚拟的圆环，如假设某哈希函数H的值空间为0-2^32-1（即哈希值是一个32位无符号整形），整个哈希环如下：

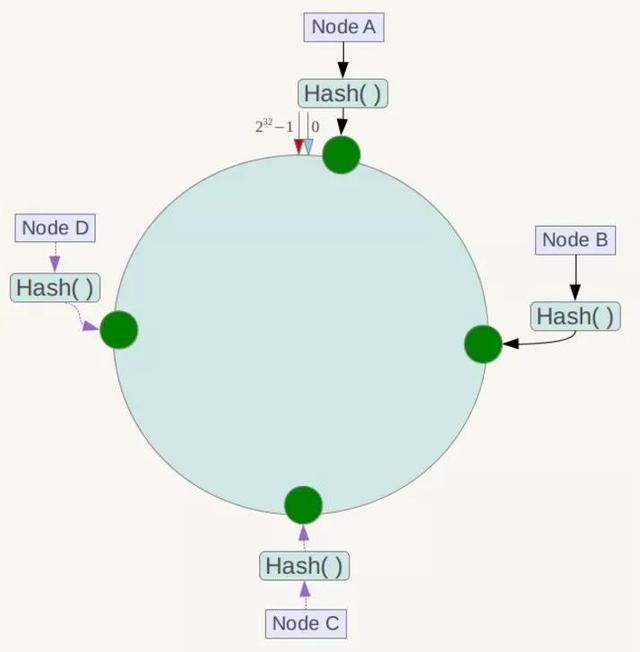
整个空间按顺时针方向组织，圆环的正上方的点代表0，0点右侧的第一个点代表1，以此类推，2、3、4、5、6……直到2^32-1，也就是说0点左侧的第一个点代表2^32-1， 0和2^32-1在零点中方向重合，我们把这个由2^32个点组成的圆环称为Hash环。

那么，一致性哈希算法与上图中的圆环有什么关系呢？假设我们有4台缓存服务器，Node A、Node B、Node C，Node D，这4台服务器有自己的IP地址或主机名，使用它们各自的IP地址或主机名作为关键字进行哈希计算，使用哈希后的结果对2^32取模，使用如下公式:

hash（服务器IP地址） % 2^32

通过上面公式算出的计算得到一个0到2^32-1之间的整数，在hash环上必定有一个点与这个整数对应，那么，这台服务器就可以映射到这个环上了，其他服务器一次类推即可得到相应的位置。

同时，将数据Object使用相同的函数Hash计算出哈希值，并确定此数据在环上的位置，从此位置沿环顺时针“行走”，遇到的第一台服务器就是该数据应该映射到的服务器，

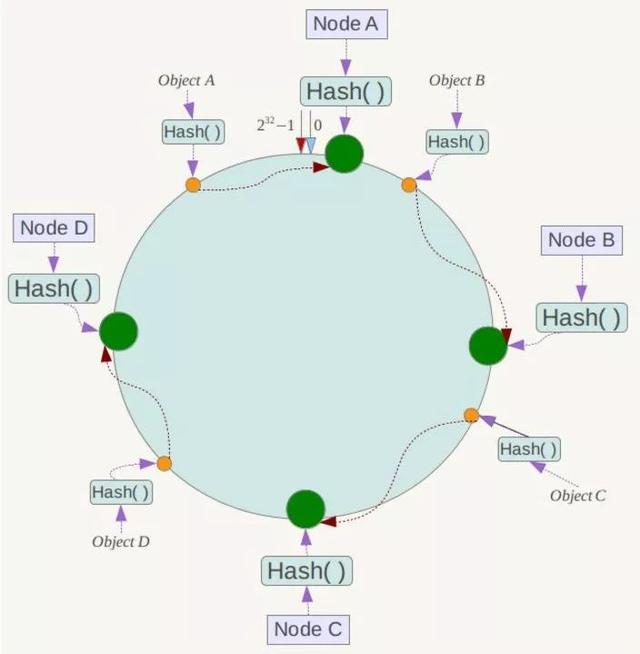
容错性和可扩展性

现假设Node C不幸宕机，可以看到此时对象A、B、D不会受到影响，只有C对象被重定位到Node D。一般的，在一致性Hash算法中，如果一台服务器不可用，则受影响的数据仅仅是此服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它不会受到影响，如图所示：

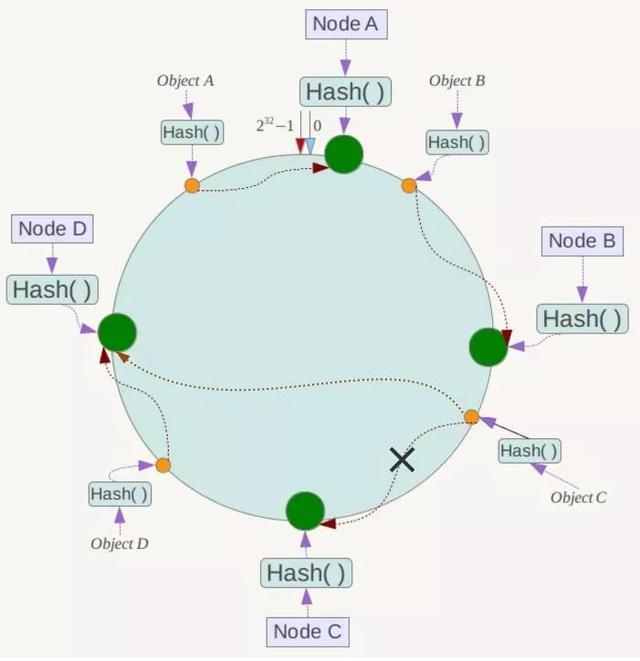
下面考虑另外一种情况，如果在系统中增加一台服务器Node X，如下图所示：

此时对象Object A、B、D不受影响，只有对象C需要重定位到新的Node X ！一般的，在一致性Hash算法中，如果增加一台服务器，则受影响的数据仅仅是新服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它数据也不会受到影响。

综上所述，一致性Hash算法对于节点的增减都只需重定位环空间中的一小部分数据，具有较好的容错性和可扩展性。

虚拟节点

一致性Hash算法在服务节点太少时，容易因为节点分部不均匀而造成数据倾斜（被缓存的对象大部分集中缓存在某一台服务器上）问题，例如系统中只有两台服务器，其环分布如下hash:

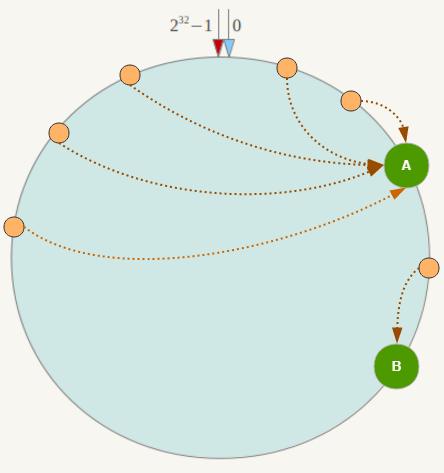
此时必然造成大量数据集中到Node A上，而只有极少量会定位到Node B上。为了解决这种数据倾斜问题，一致性Hash算法引入了虚拟节点机制，即对每一个服务节点计算多个哈希，每个计算结果位置都放置一个此服务节点，称为虚拟节点。具体做法可以在服务器IP或主机名的后面增加编号来实现。

例如上面的情况，可以为每台服务器计算三个虚拟节点，于是可以分别计算 “Node A#1”、“Node A#2”、“Node A#3”、“Node B#1”、“Node B#2”、“Node B#3”的哈希值，于是形成六个虚拟节点hash:

同时数据定位算法不变，只是多了一步虚拟节点到实际节点的映射，例如定位到“Node A#1”、“Node A#2”、“Node A#3”三个虚拟节点的数据均定位到Node A上。这样就解决了服务节点少时数据倾斜的问题。在实际应用中，通常将虚拟节点数设置为32甚至更大，因此即使很少的服务节点也能做到相对均匀的数据分布。