Burton Howard Bloom 在 1970 年提出了一个叫做 Bloom Filter（中文翻译：布隆过滤）的算法。它主要就是用于解决判断一个元素是否在一个集合中，但它的优势是只需要占用很小的内存空间以及有着高效的查询效率。相比于传统的 List、Set、Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的。

算法原理

布隆过滤器（BloomFilter）由一个很长的二进制向量和一系列抗碰撞的Hash函数组成， 可以用于快速判断一个元素是否在一个集合中。优点：空间仅由二进制向量决定，并且查询时间远超一般算法（仅需计算k 个Hash函数的值）；**缺点：**有一定的错误识别率，并且一旦元素被添加到布隆过滤器中就很难再将该元素从布隆过滤器中删除。

初始状态时，BloomFilter是一个长度为***m*** 的比特数组（二进制向量），每一位都置为0。

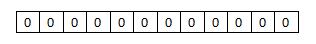
把1个新元素***x*** 添加进BloomFilter，对***x*** 计算***k*** 个散列函数哈希值（哈希值作为比特数组的下标），将比特数组中对应位设置为1。

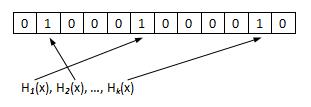
判断元素***y*** 是否存在于BloomFilter中，对***y*** 计算***k*** 个散列函数哈希值，若对应位置的位皆为1，则说明y 存在于BloomFilter中。

实例

这样说可能比较抽象，举个例子：

我们假设 K 是 2，有 Hash1 和 Hash2 两个哈希函数

Hash1 = n%3
Hash2 = n%8

然后我们创建一个名叫 bitMap 长度是 20 的位图

bitMap=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这个时候，我们要将 7，存入到这个集合中

n = 7

分别用 Hash1 和 Hash2 计算 n 哈希后的值

Hash1  ->  1
Hash2  ->  7

我们把 bitMap 对应的值置为 1，从 0 开始

bitMap=[0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这样下次我们来查找 7 在不在这个集合的时候就可以用 Hash1 和 Hash2 计算完以后在 bitMap 集合中查找对应位置是否都是 1，如果都是 1 则一定在集合中。

如果再在集合中插入 13 分别用 Hash1 和 Hash2 计算 n 哈希后的值

n = 13
Hash1  ->  1
Hash2  ->  5

我们把 bitMap 对应的值置为 1，从 0 开始

bitMap=[0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

这个时候我们发现 1 被映射到了两次，但是并不影响我们在集合 [7, 13] 中快速找到 7 或者 13。

但是当插入的数据量大幅提升的时候，甚至 bitMap 全部被置为 1 的时候问题就很严重了，误识率就非常高了，这个也是根据不同场景实现布隆过滤器所要考虑的问题。

尽管有这样的问题，但是仍然不能掩盖布隆过滤器的空间利用率和查询时间远超其他算法，插入数据和查询数据的时间复杂度都是 O (k)

算法实现

/**
 * MurmurHash
 * 
 * 参考 http://murmurhash.googlepages.com/ 
 * 
 * data：待哈希的值
 * offset：
 * seed：种子集
 *
 */
function MurmurHash (data, offset, seed) {
    let len = data.length,
      m = 0x5bd1e995,
      r = 24,
      h = seed ^ len,
      len_4 = len >> 2;  

  for (let i = 0; i < len_4; i++) {  
      let i_4 = (i << 2) + offset,
          k = data[i_4 + 3];

      k = k << 8;  
      k = k | (data[i_4 + 2] & 0xff);  
      k = k << 8;  
      k = k | (data[i_4 + 1] & 0xff);  
      k = k << 8;  
      k = k | (data[i_4 + 0] & 0xff);  
      k *= m;  
      k ^= k >>> r;  
      k *= m;  
      h *= m;  
      h ^= k;  
  }  
  
  // avoid calculating modulo  
  let len_m = len_4 << 2,
      left = length - len_m,
      i_m = len_m + offset;  

  if (left != 0) {  
      if (left >= 3) {  
          h ^= data[i_m + 2] << 16;  
      }  
      if (left >= 2) {  
          h ^= data[i_m + 1] << 8;  
      }  
      if (left >= 1) {  
          h ^= data[i_m];  
      }  

      h *= m;  
  }  

  h ^= h >>> 13;  
  h *= m;  
  h ^= h >>> 15;  

  return h;  
}


/**
 * BoolmFilter
 * maxKeys：最大数量
 * errorRate：错误率
 *
 */
function BoolmFilter (maxKeys, errorRate) {
  // 布隆过滤器位图映射变量
  this.bitMap = [];
  // 布隆过滤器中最多可放的数量
  this.maxKeys = maxKeys;
  // 布隆过滤器错误率
  this.errorRate = errorRate;
  // 位图变量的长度，需要根据maxKeys和errorRate来计算
  this.bitSize = Math.ceil(maxKeys * (-Math.log(errorRate) / (Math.log(2) * Math.log(2)) ));
  // 哈希数量
  this.hashCount = Math.ceil(Math.log(2) * (this.bitSize / maxKeys));
  // 已加入元素数量
  this.keyCount = 0;

  // 初始化位图数组
  // for (let i = Math.ceil(this.bitSize / 31) - 1; i >=0; i--) {
  //   this.bitMap[i] = 0;
  // }
}

/**
 * 设置位
 *
 */
BoolmFilter.prototype.bitSet = function (bit) {
  // this.bitMap |= (1<<bit);
  // bitSize
  let numArr = Math.floor(bit / 31),
      numBit = Math.floor(bit % 31);
  this.bitMap[numArr] |= (1<<numBit);
  // this.bitMap[bit] = 1;
}

/**
 * 读取位
 *
 */
BoolmFilter.prototype.bitGet = function (bit) {
  // return this.bitMap &= (1<<bit);
  let numArr = Math.floor(bit / 31),
      numBit = Math.floor(bit % 31);
  return this.bitMap[numArr] &= (1<<numBit);
  // return this.bitMap[bit];
}

/**
 * 加入布隆过滤器
 *
 */
BoolmFilter.prototype.add = function (key) {
  if (this.contain(key)) {
    return -1;
  }

  let hash1 = MurmurHash(key, 0, 0),
      hash2 = MurmurHash(key, 0, hash1);  
  
  for (let i = 0; i < this.hashCount; i++) {
    this.bitSet(Math.abs( Math.floor((hash1 + i * hash2) % (this.bitSize)) ));  
  }  
  
  this.keyCount++;
}

/**
 * 检测是否已经存在
 *
 */
BoolmFilter.prototype.contain = function (key) {
  let hash1 = MurmurHash(key, 0, 0),
      hash2 = MurmurHash(key, 0, hash1);  
  
  for (let i = 0; i < this.hashCount; i++) {  
    if ( !this.bitGet(Math.abs( Math.floor((hash1 + i * hash2) % (this.bitSize)) )) ) {
      return false;
    }  
  }

  return true;
}

应用场景

布隆过滤器被广泛用于网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统以及解决缓存穿透问题。通过介绍已经知晓布隆过滤器的作用是检索一个元素是否在集合中。可能有人认为这个功能非常简单，直接放在redis中或者数据库中查询就好了。又或者当数据量较小，内存又足够大时，使用hashMap或者hashSet等结构就好了。但是如果当这些数据量很大，数十亿甚至更多，内存装不下且数据库检索又极慢的情况，我们应该如何去处理？这个时候我们不妨考虑下布隆过滤器，因为它是一个空间效率占用极少和查询时间极快的算法，但是需要业务可以忍受一个判断失误率。