图（Graph）结构是一种非线性的数据结构，图在实际生活中有很多例子，比如交通运输网，地铁网络，社交网络，计算机中的状态执行（自动机）等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。

图的结构

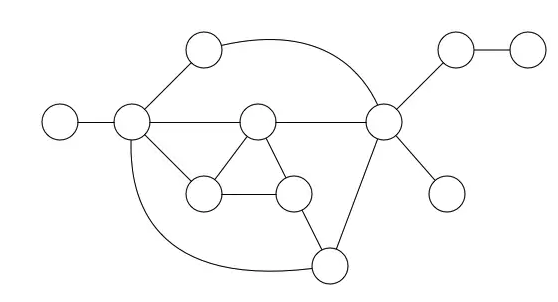
一个图G=(V, E)由以下元素组成：

• **顶点（vertex，V）：**图中的数据元素
• **边（edge，E）：**图中连接这些顶点的线

所有的顶点构成一个顶点集合，所有的边构成边的集合，一个完整的图结构就是由顶点集合和边集合组成。

由一条边连接在一起的顶点称谓相邻顶点，一个顶点的度是其相邻顶点的数量。

有向图/无向图

无向图

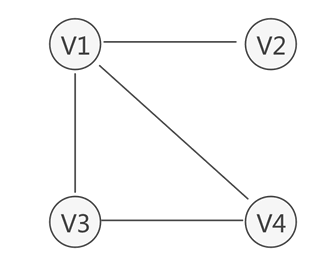
如果一个图结构中，所有的边都没有方向性，那么这种图便称为无向图。典型的无向图，如图所示。由于无向图中的边没有方向性，这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V2之间的边，可以表示为(V1， V2),也可以表示为(V2，V1)。

有向图

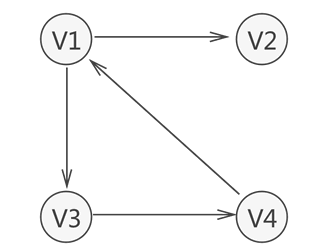
一个图结构中，边是有方向性的，那么这种图就称为有向图，如图三所示。由于图的边有方向性，我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边，例如<V1，V2>表示从顶点V1到顶点V2，而<V4，V1>表示顶点V4到顶点V1。

图的表示

理论上，图就是一堆顶点和边对象而已，但是怎么在代码中来描述呢？

有两种主要的方法：邻接列表和邻接矩阵。

邻接列表

在邻接列表实现中，每一个顶点会存储一个从它这里开始的边的列表。比如，如果顶点A 有一条边到B、C和D，那么A的列表中会有3条边。

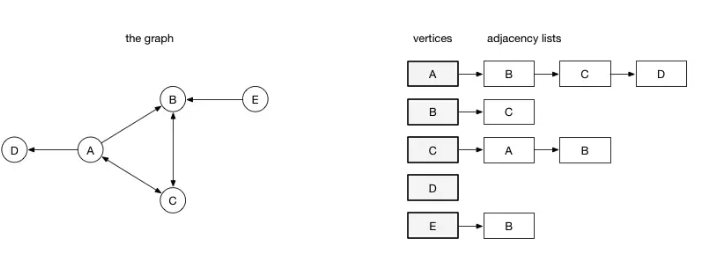
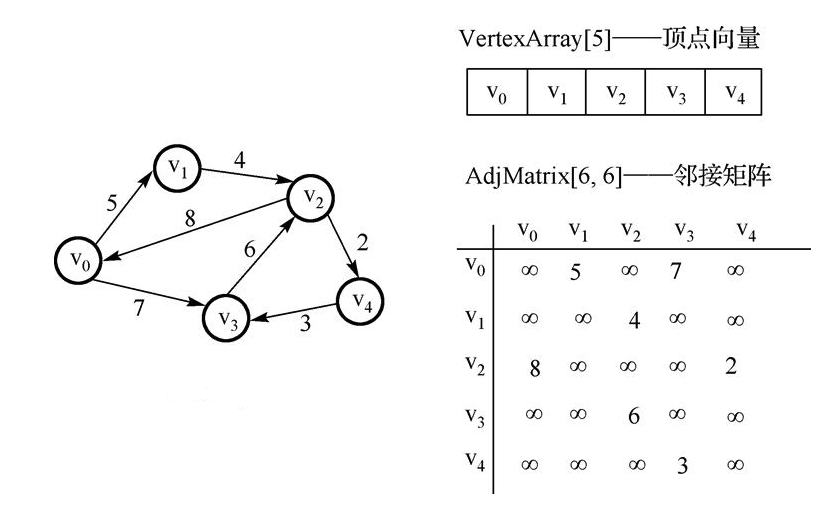
邻接矩阵

在邻接矩阵实现中，由行和列都表示顶点，由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连。

代码实现

以邻接列表为例，我们实现一个图类。使用一个数组来存储图中所有的顶点的名字，以及一个字典来存储邻结表，字典使用顶点的名称作为键，邻接顶点列表作为值。

function Graph() {
	var vertices = [];
	var adjList = {};

	this.addVertex = function(v) {
		vertices.push(v);
		adjList[v] = [];
	}

	this.addEdge = function(v, w) {
		adjList[v].push(w);
		adjList[w].push(v);
	}
}

图的遍历

有两种算法可以对图进行遍历：广度优先搜索（Breadth-First Search, BFS) 和深度优先搜索（Depth-First Search, DFS)。

图遍历算法的思想是追踪每个第一次访问的节点，并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法，都需要明确指出第一个被访问的节点。完全探索一个顶点要求我们查看该顶点的每一条边，对于每一条边所连接的没有被访问过的顶点，将其标注为被发现状态，并将其加进待访问顶点列表中。

为了保证算法的效率，每个顶点最多访问两次。

广度优先搜索

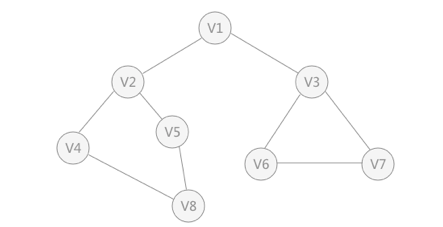
广度优先搜索类似于树的层次遍历。从图的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。

最后还需要做的操作就是查看图中是否存在尚未被访问的顶点，若有，则以该顶点为起始点，重复上述遍历的过程。

以上无向图为例，假设 V1 作为起始点，遍历其所有的邻接点 V2 和 V3 ，以 V2 为起始点，访问邻接点 V4 和 V5 ，以 V3 为起始点，访问邻接点 V6 、 V7 ，以 V4 为起始点访问 V8 ，以 V5 为起始点，由于 V5 所有的起始点已经全部被访问，所有直接略过， V6 和 V7 也是如此。

V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> V8

代码实现：

// 初始化所有顶点，标记为未被访问状态
this.initFlags = function() {
		var flags = [];
		for(var i = 0; i < vertices.length; i++) {
			flags[vertices[i]] = 0;
		}
		return flags;
	}

	this.bfs = function(v) {
		var flags = initFlags(), queue = new Queue();
    // 将未访问顶点压入栈
		queue.enqueue(v);

		while(!queue.isEmpty()) {
			var u = queue.dequeue();
			var neighbors = adjList[u];
      // 将顶点标记为已访问但未探索
			flags[u] = 1;
			for (var i = 0; i < neighbors.length; i++) {
				var w = neighbors[i];
				if (flags[w] == 0) {
          flags[w] = 1;
					queue.enqueue(w);
				}
			}
      // 将顶点标记为已访问且完成探索
			flags[u] = 2;
		}
	}

深度优先搜索

深度优先搜索算法将会从第一个指定的顶点开始遍历图。沿着路径直到这条路径最后一个顶点被访问，接着原图回退并探索下一条路径。它是先深度后广度地访问顶点。

深度优先搜索的过程类似于树的先序遍历，例如上图是一个无向图，采用深度优先算法遍历这个图的过程为：

1. 首先任意找一个未被遍历过的顶点，例如从 V1 开始，由于 V1 率先访问过了，所以，需要标记 V1 的状态为访问过；
2. 然后遍历 V1 的邻接点，例如访问 V2 ，并做标记，然后访问 V2 的邻接点，例如 V4 （做标记），然后 V8 ，然后 V5；
3. 当继续遍历 V5 的邻接点时，根据之前做的标记显示，所有邻接点都被访问过了。此时，从 V5 回退到 V8 ，看 V8 是否有未被访问过的邻接点，如果没有，继续回退到 V4 ， V2 ， V1 ；
4. 通过查看 V1 ，找到一个未被访问过的顶点 V3 ，继续遍历，然后访问 V3 邻接点 V6 ，然后 V7 ；
5. 由于 V7 没有未被访问的邻接点，所有回退到 V6 ，继续回退至 V3 ，最后到达 V1 ，发现没有未被访问的；
6. 最后一步需要判断是否所有顶点都被访问，如果还有没被访问的，以未被访问的顶点为第一个顶点，继续依照上边的方式进行遍历。

根据上边的过程，可以得到上图通过深度优先搜索获得的顶点的遍历次序为：

V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7。

代码实现：

this.initFlags = function() {
		var flags = [];
		for(var i = 0; i < vertices.length; i++) {
			flags[vertices[i]] = 0;
		}
		return flags;
	}

	this.dfs = function() {
		var flags = this.initFlags();
		for (var i = 0; i < vertices.length; i++) {
			if (flags[vertices[i]] == 0) {
				this.dfsvisit(vertices[i], flags);
			}
		}
	}

	this.dfsvisit = function(u, flags) {
		flags[u] = 1;
		console.log(u);
		var neighbors = adjList[u];
		for (var i = 0; i < neighbors.length; i++) {
			var w = neighbors[i];
			if (flags[w] == 0) {
				this.dfsvisit(w, flags);
			}
		}
		flags[u] = 2;
	}

全部代码

/ 队列
function Queue() {

	let items = [];

	this.enqueue = function(element) {
		items.push(element);
	}

	this.dequeue = function() {
		return items.shift();
	}

	this.front = function() {
		return items[0];
	}

	this.isEmpty = function() {
		return items.length == 0;
	}

	this.toString = function() {
		return items.toString();
	}
}

// 图
function Graph() {
	var vertices = [];
	var adjList = {};

	this.addVertex = function(v) {
		vertices.push(v);
		adjList[v] = [];
	}

	this.addEdge = function(v, w) {
		adjList[v].push(w);
		adjList[w].push(v);
	}

	this.initFlags = function() {
		var flags = [];
		for(var i = 0; i < vertices.length; i++) {
			flags[vertices[i]] = 0;
		}
		return flags;
	}

	this.bfs = function(v) {
		var flags = this.initFlags(), queue = new Queue();
		queue.enqueue(v);

		while(!queue.isEmpty()) {
			var u = queue.dequeue();
			var neighbors = adjList[u];
			flags[u] = 1;
			for (var i = 0; i < neighbors.length; i++) {
				var w = neighbors[i];
				if (flags[w] == 0) {
					flags[w] = 1;
					queue.enqueue(w);
				}
			}
			console.log(u);
			flags[u] = 2;
		}
	}

	this.dfs = function() {
		var flags = this.initFlags();
		for (var i = 0; i < vertices.length; i++) {
			if (flags[vertices[i]] == 0) {
				this.dfsvisit(vertices[i], flags);
			}
		}
	}

	this.dfsvisit = function(u, flags) {
		flags[u] = 1;
		console.log(u);
		var neighbors = adjList[u];
		for (var i = 0; i < neighbors.length; i++) {
			var w = neighbors[i];
			if (flags[w] == 0) {
				this.dfsvisit(w, flags);
			}
		}
		flags[u] = 2;
	}

	this.toString = function() {
		var s = '';
		for(var i = 0; i < vertices.length; i++) {
			s += vertices[i] + ' -> ';
			var neighbors = adjList[vertices[i]];
			for (var j = 0; j < neighbors.length; j++) {
				s += neighbors[j] + ' ';
			}
			s += '\n';
		}
		return s;
	}	
}