题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

解题思路

题目可能比较难理解，可以看如下的图，我们有一棵二叉搜索树，要求得右边的双向链表。

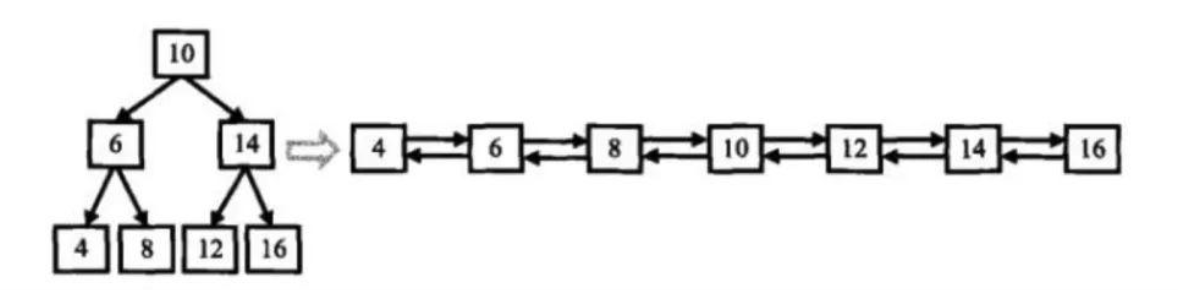
在二叉搜索树中，左子结点的值总是小于父结点的值，右子节点的值总是大于父结点的值。因此我们在转换成排序双向链表时，原先指向左子结点的指针调整为链表中指向前一个结点的指针，原先指向右子节点的指针调整为链表中指向后一个结点的指针。由于要求链表是有序的，可以借助二叉树中序遍历，因为中序遍历算法的特点就是从小到大访问结点。当遍历访问到根结点时，假设根结点的左侧已经处理好，只需将根结点与上次访问的最近结点（左子树中最大值结点）的指针连接好即可。进而更新当前链表的最后一个结点指针。同时中序遍历过程正好是转换成链表的过程，可采用递归方法处理。

代码实现

/**
 * 双向链表节点
 */
class DLNode {
	public $data;
	public $next; // 指向下一个节点
	public $prev; // 指向前一个节点

	public function __construct($data) {
		$this->data = $data;
		$this->next = null;
		$this->prev = null;
	}
}

class DoubleLinkedList {
	private $head;

	public function append($data) {
		$node = new DLNode($data);
		if ($this->head == null) {
			$this->head = $node;
		} else {
			$this->appendNode($this->head, $node);
		}
	}

	private function appendNode($node, $newNode) {
		if ($node->next == null) {
			$node->next = $newNode;
			$newNode->prev = $node;
		} else {
			$this->appendNode($node->next, $newNode);
		}
	}

	public function toString() {
		$str = $this->head->data;
		$current = $this->head->next;

		while ($current) {
			$str .= ','.$current->data;
			$current = $current->next;
		}

		return $str;
	}
}

/**
* 将二叉搜索树转换成一个排序的双向链表
*/
public function convertDLinked() {
  $dlink = new DoubleLinkedList();
  $this->convertDLinkedNode($this->root, $dlink);
  return $dlink;
}

private function convertDLinkedNode($node, $dlink) {
  if ($node != null) {
    $this->convertDLinkedNode($node->left, $dlink);
    $dlink->append($node->data);
    $this->convertDLinkedNode($node->right, $dlink);
  }
}