列表、栈、队列都是线性的数据结构，对应的还有非线性数据结构，其中**树（tree)**是比较常见的非线性数据结构。

在树结构中，每个节点都有一个前节点(父节点），有一个或者多个后节点（子节点）。没有父节点的节点称为根节点，没有子节点的节点称为叶子节点。一个结点所拥有的子结点的个数称为该结点的度，所有结点中最大的度称为树的度。树的最大层次称为树的深度。

二叉树是一种最简单的数结构，它的子节点个数不超过两个，分别称为该结点的左子树与右子树。

节点的结构

节点是由节点保存的数据和指向左右树的指针组成，我们可以这么定义一个节点类：

function Node(data) {
	this.data = data;
	this.left = null; // 左节点
	this.right = null; // 有节点
}

节点插入

当我们新的节点要插入树时，肯定会有一个思考: 插在左边或者右边，还是乱序？所以我们一般在插入节点的事情会提前确定一个插入标准， 通常将相对较小的值保存在左节点中，较大的值保存在右节点中，这就使得查找的效率非常高，因此被广泛使用。

function Tree() {
	this.root = null; // 根节点

	this.insert = function(data) {
		var node = new Node(data);
		if (!this.root) {
			 this.root=node;
		} else {
			var current = this.root;
			var parent;
			while (true) {
				parent = current;
				// 插入的节点与所有的节点的值进行比较，当大于当前节点的值，则插到左边，当小于当前节点的值，则插到右边，我们搜索时也采用统一的比较规则，快速找到节点位置
				if (data < current.data) {
					current = current.left;
					if (current == null) {
						parent.left = node;
						break;
					}
				} else {
					current = current.right;
					if (current == null) {
						parent.right = node;
						break;
					}
				}
			}
		}
	} 
}

节点查找

节点查找可以按照节点插入规律：小左大右，依次循环比较每个节点的值和查找值，直到找到节点值和查找值一致的节点。

this.find = function(value) {
	var current = this.root;
	while (current != null) {
		if (current.data < value) {
			current = current.right;
		} else if (current.data > value) {
			current = current.left;
		} else {
			return current;
		}
	}

	return null;
}

遍历

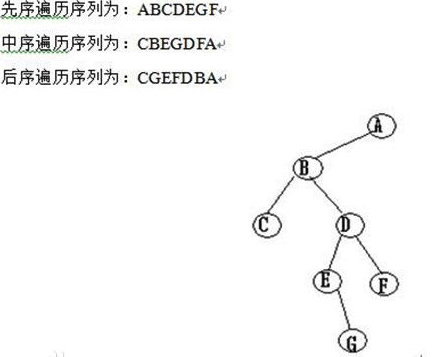
按照根节点访问的顺序不同，树的遍历分为以下三种：

• 前序遍历：根->左->右
  1. 访问根节点
  2. 前序遍历左节点
  3. 前序遍历右节点
• 中序遍历：左->根->右
  1. 中序遍历左节点
  2. 访问根节点
  3. 中序遍历右节点
• 后序遍历：左->右->根
  1. 后序遍历左节点
  2. 后序遍历右节点
  3. 访问根节点

// 前序遍历，根左右
this.preOrder = function(node) {
	if (node != null) {
		console.log(node.data);
		this.preOrder(node.left);
		this.preOrder(node.right);
	}
}

// 中序遍历，左根右
this.inOrder = function(node) {
	if (node != null) {
		this.inOrder(node.left);
		console.log(node.data);
		this.inOrder(node.right);
	}
}

// 后序遍历，左右根
this.postOrder = function(node) {
	if (node != null) {
		this.postOrder(node.left);
		this.postOrder(node.right);
		console.log(node.data);
	}
}

二叉树的遍历是递归的典型运用场景。

查找最小值

根据插入的规则，最大的值应该在最左的叶子节点，因此，我们只需要遍历左子树，只到左子树left为null;

// 根据插入规则，最左的值，应该是最小值
this.getMin = function() {
	var current = this.root;
	while (current.left != null) {
		current = current.left;
	}
	return current.data;
}

查找最大值

根据插入的规则，最大的值应该在最右的叶子节点，因此，我们只需要遍历右子树，只到右子树right为null;

// 根据插入规则，最右的值，应该是最大值
this.getMax = function() {
	var current = this.root;
	while (current.right != null) {
		current = current.right;
	}
	return current.data;
}

完整代码

// 二叉树

function Node(data) {
	this.data = data;
	this.left = null; // 左节点
	this.right = null; // 有节点
}

function Tree() {
	this.root = null; // 根节点

	this.insert = function(data) {
		var node = new Node(data, null, null);
		if (!this.root) {
			 this.root=node;
		} else {
			var current = this.root;
			var parent;
			while (true) {
				parent = current;
				if (data < current.data) {
					current = current.left;
					if (current == null) {
						parent.left = node;
						break;
					}
				} else {
					current = current.right;
					if (current == null) {
						parent.right = node;
						break;
					}
				}
			}
		}
	} 

	// 前序遍历，根左右
	this.preOrder = function(node) {
		if (node != null) {
			console.log(node.data);
			this.preOrder(node.left);
			this.preOrder(node.right);
		}
	}

	// 中序遍历，左根右
	this.inOrder = function(node) {
		if (node != null) {
			this.inOrder(node.left);
			console.log(node.data);
			this.inOrder(node.right);
		}
	}

	// 后序遍历，左右根
	this.postOrder = function(node) {
		if (node != null) {
			this.postOrder(node.left);
			this.postOrder(node.right);
			console.log(node.data);
		}
	}

	this.find = function(value) {
		var current = this.root;
		while (current != null) {
			if (current.data < value) {
				current = current.right;
			} else if (current.data > value) {
				current = current.left;
			} else {
				return current;
			}
		}

		return null;
	}

	// 根据插入规则，最左的值，应该是最小值
	this.getMin = function() {
		var current = this.root;
		while (current.left != null) {
			current = current.left;
		}
		return current.data;
	}

	// 根据插入规则，最右的值，应该是最大值
	this.getMax = function() {
		var current = this.root;
		while (current.right != null) {
			current = current.right;
		}
		return current.data;
	}
}